In our previous post on the eGrader campaign we discussed its technological and political strategy, the true nature of the eGrader algorithm, and how climbing elites attempting to prescribe their beliefs on to others is undemocratic, aristocratic and authoritarian.
In this post we switch our attention to the empirical and address the scientific evidence presented by the eGrader campaign in support of the abolition of the existing British trad grading scale and its replacement with the eGrader spreadsheet. The campaign has made this argument three times in three places: by Tom Randall, by James Pearson and on the eGrader instagram page. The fact this argument has been repeated three times suggests they really do believe it.
First thing to note is that commenters on these posts have been taking the presented argument as hard statistical evidence underlying the legitimacy of the eGrader, and providing the normative reason for the abolition of the existing system. Indeed, if it is not meant to be taken seriously then why post the argument at all?
A second, arguably more important, reason to assess its scientific validity is that the implications of their conclusions are so large: i.e. abolition and replacement of the British traditional grading scale. Indeed, members of the eGrader campaign team Neil Gresham1 and Steve Mcclure2 have argued that the eGrader now has the final word in grading British traditional rock climbs. As a rule, if your research leads you to make a prescriptive claim (i.e. asserting you know better than others and that they should do what you say) you better be damn sure both your data and your methodology are rock-solid.
We did think about having this matter adjudicated by Tim Harford at BBC Radio 4’s More or Less, and perhaps he will yet take up the issue for us, but in the meantime we shall crack on ourselves. Now, we do not climb E9, so in this sense we are not peers of the eGrader campaign team athletes and so cannot reasonably comment on their subjective experiences and consequent grading decisions. However, the eGrader campaign’s argument is a statistical one, an area where we might be able to offer some insight. We are therefore going to subject the eGrader’s scientific argument to something akin to peer review.3 So let us pretend they have submitted this argument to a journal, for which we are a reviewer, and it has landed on our desk.
Before we begin let us first define some key terms the audience may wish to keep in mind while reading this post. We will not come to firm conclusions as to which, if any, of these terms apply; this exercise is left for the reader.
Bad science is a flawed version of good science, with the potential for improvement. It follows the scientific method, only with errors or biases. Often, it’s produced with the best of intentions, just by researchers who are responding to skewed incentives.
Pseudoscience has no basis in the scientific method. It does not attempt to follow standard procedures for gathering evidence. The claims involved may be impossible to disprove. Pseudoscience focuses on finding evidence to confirm it, disregarding disconfirmation. Practitioners invent narratives to preemptively ignore any actual science contradicting their views. It may adopt the appearance of actual science to look more persuasive.4
Data Issues (Garbage In, Garbage Out)
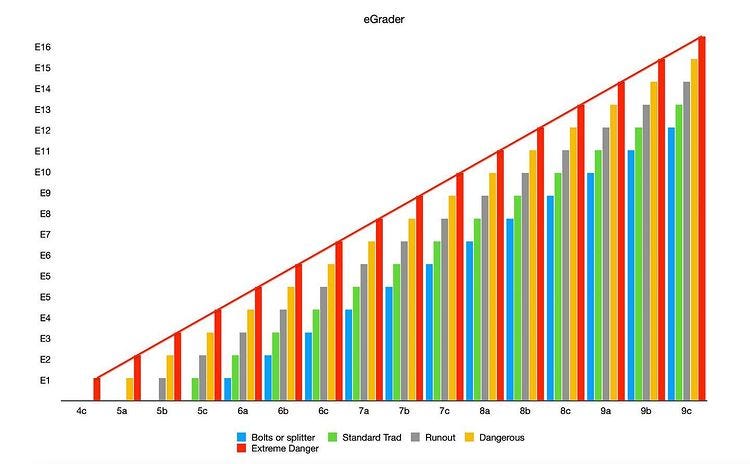
In this section we address the nature of Figure 1, the basis of the eGrader campaign’s argument. We will refrain from analysing Figure 2 as it does not represent real data; it is merely an infographic displaying how their spreadsheet works.5
So what does the eGrader campaign claim Figure 1 shows? They simply claim that it is a bar graph based on a sample of routes across the whole “danger spectrum”. However, the conclusions that can be drawn from a statistical model are only as good as the data it is based on: if garbage goes in, then what comes out will also be garbage. It is therefore crucial to note that the data table upon which Figure 1 is based has not been released to the public.6 Independent analysts can therefore not use this data to confirm or dispute their analysis and conclusions.
So given that we are unable to replicate the analysis, our next best option is to point out all the additional things we would need to know that would indicate that the eGrader campaign’s conclusions might possibly be scientifically valid. This is a problem because there are so many things we do not know. Indeed, it is unscientific in of itself to assert the validity and normative value of their conclusions without adequately explaining their methodology.
The following unanswered questions are immediately obvious. In their absence we are unable to rule-out the possibility that the routes selected have been cherry-picked to fit desired conclusions.
Which routes were included in the sample?
What is the statistical population from which the routes were sampled?
Is the sample random?
If not, who selected these routes? On what basis were they selected?
Did the people who selected this sample of routes have a vested interest in the outcome of the research?
Another thing that is not clear is whether each bar is an individual route or the mean average of several routes. If each bar is an individual route then the whole analysis is bogus right from the off. You cannot draw a conclusion on the true relationship between British traditional E-grades and sport grades based on a sample of only 51 routes.
Why stop at 51 routes? There are tens of thousands of traditional routes in the United Kingdom.
If each bar represents an average E-grade for routes of different sport grade and danger grade combinations then the analysis is only slightly less bogus. However, British trad grades are ordinal and not continuous, so taking a mean is questionable.7 Alternatively the bars might represent medians or some other percentile. Whichever of these is the case:
Why are confidence intervals not displayed on each bar? Without these we cannot statistically determine if the means represented by the bars are different from one another. We therefore cannot determine if the alleged E10 and E11 bars are outliers at all.
The following questions need to be answered regardless of whether the bars represent specific individual routes or are means, medians or percentiles of route grades. In their absence we are unable to rule-out the possibility that the data attributed to the sample of routes is not sound.
How were British traditional routes graded on the French system? How do you give gritstone routes a French grade given there are no sport routes on gritstone? Who were the people involved in grading these routes? How were they chosen? Did they have any conflicts of interest?
What standard of French grades were selected? Were all raters working by the same standard? Even adjacent regions can vary: F8a on Peak District limestone is not quite the same as F8a on Yorkshire limestone.
How were E-Grades of routes determined? Did they use guidebook data? Did they use UKClimbing consensus voting data? Did they use expert consensus?
How was the ‘danger score’ of the routes determined? Who was involved in this? How were they chosen? Did they have any conflicts of interest?
When was the danger score system formulated? Was it formulated before or after the decision to make the eGrader? Was it fine-tuned such that the analysis fit the pattern desired by the campaign?
What were the inter-rater reliability coefficients for each of the measures used (E grade, French grade, danger score)? What training was administered to raters before the data were collected? How was observer bias controlled for?
The following problems are to do with the logarithmic regression line fitted to the bars:
What is the coefficient yielded by the logarithmic regression?
Why is a confidence interval around the logarithmic regression not displayed? This is required to see if the bars at E10 and E11 are true outliers relative to the line or not. If the confidence intervals around the regression line and the E10 and E11 bars overlap, there is no evidence that these grades/routes are outliers.
Were the model fit statistics for the logarithmic regression line better than that of a linear regression? How much better were they?
What other functional forms were tested? What were the fit statistics for these?
The Python/R script used to construct the graphs and fit the logarithmic function to the data should be made public.
In summary: Figure 1 is, at best, extremely bad science. It may be a bit of a stretch to even call it scientific but it is even more of a stretch to try and justify abolishing the existing trad grading scale off the back of it. How this got past the data science team at Lattice Training we have no idea.
No wonder that Dave Macleod, probably the only British elite climber who actually understands statistics, didn’t want to touch this campaign with a bargepole. It would have been disastrous for his reputation as a practitioner of sports and nutritional science.
From Dubious Data to Dubious Hypothesis
In this section we critique the eGrader campaign’s argument that Figure 1 means that the existing British trad grading scale should be abolished and replaced with the eGrader. Here follows a direct quote detailing the argument:
As you can see, the two graphs line up almost perfectly from E1 to E7, from where the current average E grade (as things stand) begins to drop off. This is the ‘compression’ we’re discussing and why it’s so contentious to propose new E Grades, seemingly irrespective of the sheer difficulty involved.
Looking at the top graph, there are a couple of interesting examples to take note of. These are Equilibrium and Rhapsody. Both of them were “first of the grade, and have become considered benchmarks for E10 and E11 respectively. They also happen to be much more consistently aligned with the lower E Grades than other routes of E7 and above.
eGrader helps us to align the upper end E grades with these benchmarks and the rest of the E Grade spectrum, creating a more consistent progression from grade to grade.
We have explained the dubious basis of Figure 1 and therefore the E10 and E11 bars being outliers may only be so due to highly suspect statistical practices. As such, there is no guarantee they are true outliers, and yet in order for the eGrader to be justified they must be found to be outliers. Notwithstanding, for this section we will charitably ‘steel-man’ Figure 1 and assume, for the sake of argument, that it isn’t nonsense.
The eGrader team drew the following hypothesis from Figure 1: the established consensus-based British traditional grading scale is broken. So what is the basis on which they make this claim? They state that because Equilibrium and Rhapsody do not fit on the (extremely questionable) logarithmic regression line (on a plot with no confidence intervals whatsoever) this must mean that the whole scale is broken.
So does the campaign have grounds for this hypothesis? Well, in order for a hypothesis to count, there must be evidence that, if collected, would disprove it. In other words it must be falsifiable. We do think their hypothesis passes this test, because such data likely exists, it simply has not yet been collected by the campaign team, who instead relied on their dubious and mysterious sample.
The main reason to distrust the broken-scale hypothesis is that concluding that the whole scale is broken on the basis of two routes is an example of a faulty generalisation. This fallacy occurs where a conclusion is drawn about all or many instances of a phenomenon on the basis of one or a few instances of that phenomenon: “These few routes don’t fit so all other routes’ grades must be wrong!”
Another reason to distrust the hypothesis that British trad grades are broken is that the campaign team do not consider rival hypotheses for why Figure 1 looks like it does. Some alternative hypotheses that could explain this pattern might be:
The established E grades are too high for these routes. Indeed, there is some suggestion Dave Macleod may be considering downgrading Rhapsody to E10.
Equilibrium and Rhapsody are undergraded in terms of their sport grade.
The danger scores for these routes are over-estimated.
Danger scores and sport grades do not perfectly capture all the information that is taken into an account in an E grade. For example, whether the moves are secure or insecure, whether the rock is loose or solid, whether the gear is easy to place, whether you are on a remote Scottish island with no phone signal, whether you’re at Wimberry, and so on.
British trad grades do not perfectly follow mathematical rules.
British trad grades and French sport grades are not measuring the same thing and so should not be expected to be proportional at all. French grades are based on a redpoint attempt using the best sequence available. The British trad grades are based on the onsight. They are therefore measuring two fundamentally different experiences and thus are incommensurable. Just because they both have “grade” in the name does not mean they are getting at the same thing. To believe this is to commit what is known as the jingle fallacy.
Given the lack of consideration of these alternative hypotheses, particularly the first one, it is equally valid to interpret Figure 1 as an argument that Equilibrium and Rhapsody ought to be downgraded.
A final consideration is whether, even if Equilibrium and Rhapsody are true statistical outliers, that abolishing the grading scale for the rest of the traditional climbs in Britain is then the appropriate course of action. If we really must have every route fit on a single trend-line, whether logarithmic or linear8, it is surely more reasonable to modify the grades of these two routes, rather than modify the grades of potentially thousands of others.
Just a Bad Argument
In this short section we show that the eGrader campaign’s argument is a logical paradox. A paradox is an argument that derives an absurd conclusion from obviously true premises. Unfortunately for the eGrader campaign, their key argument suffers from one of these errors and is therefore logically invalid. This can clearly be seen in the following step-by-step reconstruction of their argument:
Grades arrived at by consensus are legitimate.
The grades of Rhapsody and Equilibrium have been settled by consensus.
The grades of these routes are therefore legitimate.
These routes do not fit the grade pattern ‘seen’ in the data.
The grades of other routes must therefore be incorrect, and require fixing by the eGrader, even though they were arrived at by consensus.
Grades arrived at by consensus are therefore not legitimate.
Conclusion 6 is a contradiction of Premise 1.
This argument is therefore a logical paradox.
Are Established Grades Being Vandalised?
In this section we talk about a missing piece of relevant statistical evidence, a piece that the eGrader campaign must have in their possession: the degree to which eGrader’s prescriptions differ from the established grades arrived at by democratic consensus. The eGrader campaign could easily have used their eGrader spreadsheet to calculate the ‘new-and-improved’ grades for the sample used to create Figure 1. This evidence would make for an excellent Figure 3, but alas, no such figure is provided. Even better, a new sample of routes would be collected and their concordance with the eGrader spreadsheet would be assessed. Ultimately, the degree to which the eGrader vandalises established grades is not quantified or considered at all.
Independent observers with intimate first-hand knowledge of routes they have climbed have noted that the eGrader over-grades routes by 1 to 2 E-points. This problem appears to be present across routes of multiple different areas, rock-types and styles. In order to determine whether the eGrader’s redefinition of the basis of British traditional grades has an unjustifiably large impact, we need to know what that impact is. In other words, what is the cost of forcing these outliers to fit?
Why would the eGrader campaign not provide this? One conclusion that could be drawn is that, to them, it does not matter. If the goal is to replace one system with another it would somewhat undermine your argument if the new system radically differs from the old, especially if it does so throughout the grades and not just at the top-end. People who only climb trad and have never climbed sport may soon find that the old familiar system they used to understand well is now defined in terms of a scale they have literally never used. Indeed, this would certainly indicate that the campaign’s goal is not to help make the British grading scale more comprehensible.
So if this wasn’t the goal? What was? Why do the campaign want these outliers to fit so badly? Might it be that making the outliers fit isn’t the end goal, but merely a means to a end? Could it be that the implications of the eGrader replacing the established consensus-based scale might have other desirable implications? This too is left for the reader to consider.
Conclusion
It is not democratically legitimate to exert your influence to try and change the basis of an ancient consensus-based collective creative institution. Is is especially not legitimate to do this if neither your data, nor your methodology, nor the logical structure of your argument are scientifically valid.

By the looks of it the eGrader has already failed peer review among the elite as no additional elite British athletes have declared their allegiance to the eGrader campaign. Quite the contrary in fact, Franco Cookson has objected robustly.
How to Spot Bad Science. Farnham Street.
Some data have been released in the ‘About eGrader’ pdf document. But this can’t be the data used to make Figure 1 because the pdf table does not include Equilibirum, which is stated to be in the figure.
Is it really intelligible for something to be E9.3675? Does this just mean E9? What about E8.9999? Should E8.51 be rounded up to E9? Questions abound.
It should be noted that a prior statistical analysis of the Ewbank, French, UIAA and Vermin scales — conducted by Dr Alexi Drummond and Dr Alex Popinga of the University of Auckland — found all of these to have logarithmic properties. A good argument needs to be made for why the British system ought to diverge from this international norm.